Solving Subset Sum Problem

August 29, 2016 · 4 min read

Kirtan Thakkar

Life is all about learning

I have recently came across a problem where I need to solve the subset sum problem. In this problem we have an array of numbers and we need to find the elements from the array whose sum matches a given number. You can find more details of the subset sum problem in the Wikipedia page here.

Let's start

We can solve this problem with the help of recursion. It will help us solve it with less complexity of the multiple nested loops.

For the simplicity of the understanding we will use the array [50, 40, 30, 20] and will try to find the sum=100 from the array.

So, we will start with the very first element in the array. We have 2 choices here. Either select that element or reject. Now let’s explore the possibilities in the both the options.

1. Select an element: If we select that element, then we will include that in the result list and we need to find the remaining sum from the list excluding the first element.

So, if we select 50, we need to find the remaining sum (i.e. 100-50: 50) from the array excluding first element (i.e. [40, 30, 20])

2. Reject an element: If we don’t select the element, then we will not include it in the result list and we need to find the sum exactly the same from the remaining list after excluding the element we rejected.

So, it we don’t select 50, we need to find the same sum (i.e. 100) from the array excluding first element. (i.e. [40, 30, 20])

This causes 2 types of possibilities in each step of the recursion. Select or Reject the first element. This will cause a binary tree with the possibilities like this:

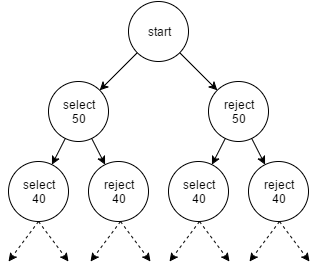
In each path at the end, all the selected elements in that path will be the answer to our problem.

Now, let’s talk about how and where do we end in this recursion loop.

###Breaking or Ending the recursion:

Before deciding the path of selecting or rejecting first element, check if the requested sum equals 0 or not. If sum=0, then we have found our way and break it. Else we have still need to go and continue.

One other check we can make is if we exceeded the value required for the sum. Whenever we select an element we subtract that value from the sum and pass it forward. So, if the sum is less than 0, then there is no point of going forward, and break the loop. This will improve the performance.

At last, if we reached to the end and still sum != 0, then we can break as this path failed to find a solution.

So, this 3 checks will help us break the loop in case where we find a solution, or there won’t be a solution going forward.

###Let’s code

The following function is a Java function and will return the path in the result variable. It is simple to understand.

Whenever we select an element we add it to the result. We remove it, if that path fails to find a solution with that element selected and goes with rejecting that element.

This will return the very first path it finds, which solves our problem.

SubsetSumProblem.java

    public static boolean findSumFromList (ArrayList<Integer> set, Integer sum, ArrayList<Integer> result) {
        // if sum=0, we have found a solution
        if (sum == 0) {
            System.out.println(result);
            return true;
        }

        // Sum < 0. No point going forward in the path
        if (sum < 0)
            return false;

        // Reached at the end of a path and this path is not the solution
        if (set.size() == 0 && sum != 0)
            return false;


        ArrayList<Integer> newSet = new ArrayList<>(set);
        newSet.remove(0);

        // Select the first element
        System.out.println("Left: Picking up " + set.get(0));
        result.add(set.get(0));
        if (findSumFromList(newSet, sum - set.get(0), result)) {
            return true;
        }

        // Reject the first element
        System.out.println("Right: NOT Picking up " + set.get(0));
        result.remove(result.size()-1);
        if (findSumFromList(newSet, sum, result)) {
            return true;
        }

        return false;
    }

The following diagram shows set of variables passed as we reach go in each recursion:

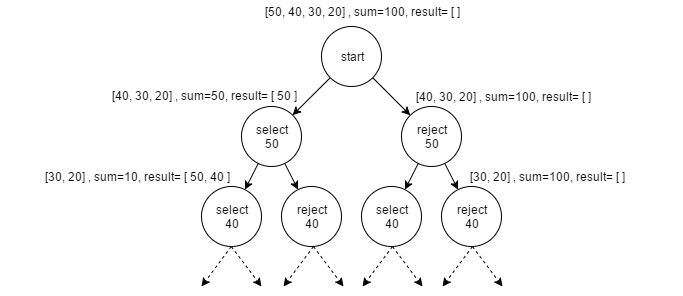
The values for the middle nodes is not included because of the space issues.

So, here we got the result: [50,30,20].

Try to play with the different arrays for input set to get the different outputs.

If we provide the array in ascending or descending order, it will ensure we get the same result every time. Because there can be more than 1 solution for the given array. But, putting it in order will provide the same result providing the same set.

Happy coding!

Let's start#

Let's start